| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
- oracle
- 파이썬
- Python
- 스프링 부트
- 컬렉션 인터페이스
- 완주하지못한선수
- db
- 사이킷런 회귀
- WinError5
- Selenium
- 차원증가
- 셀레니움
- 쓰레드 풀
- Java
- openai
- 프로그래머스
- 오라클
- 스프링 부트3
- 컬렉션 프레임웍
- 자바 로그 레벨
- 알고리즘
- h2 데이타베이스
- 자바 열거형
- conda remove
- GIT
- URI 원칙
- 사이킷런
- REST API
- 머신러닝
- streamlit
- Today
- Total
노트 :
이진 분류 성능 지표 - 정확도, 혼동 행렬(AKA 오차 행렬), ROC곡선 본문
1. 정확도(Accuracy)
혼동 행렬을 알기 위해서는 정확도에 대해 알아야 한다.
정확도는 예측 데이터가 얼마나 정확하게 예측했는 지 나타내는 지표이다.계산법은 아래와 같다.

정확도는 개념과 사용법이 단순하므로 편하게 사용할 수 있다.
그러나 이진 분류 모델의 데이터의 구성에 따라 정확도가 정확하지 않은 지표가 될 수 있다.
예를 들어보자.
코로나 바이러스에 걸린 환자(positive, 1)와 걸리지 않은 정상인(negative, 0)으로 이루어진 데이터가 있다.
새로운 환자의 코로나 바이러스 감염 여부를 확인하고자 할 때, 분류 모델이 예측을 계속해서 '0'으로만 내려도 정확도가 높을 것이다. 여러 변수를 고려하여 정밀 예측을 한 분류 모델보다 정확도가 더 높을 수 있는 이상한 상황이 발생할 수도 있는 것이다.
2. 혼동 행렬(Confusion matrix)
이진 분류모델에서의 정확도의 정확하지 않음(?)을 극복한 성능 지표가 혼동 행렬이다.
혼동 행렬은 오차 행렬이라고 불리기도 한다.
혼동 행렬은 2x2의 행렬로 분류 모델의 예측 값과 실제 값을 비교하여 TP, FN, FP, TN으로 표현한다.

2-1. 정확도(Accuracy)
앞서 정의했던 정확도를 혼동 행렬을 이용해서 다시 재정의해보자.
Accuracy = (TP + TN) / (TP + FN + FP + TN)정확도를 사용하려면, 데이터의 분포가 불균형하지 않아야 한다.
병의 발생여부, 신용카드 부정사용 여부 등 데이터의 분포가 불균형하다면 사용해서는 안 된다.
2-2. 정밀도(Precision)
분류 모델이 positive로 예측한 데이터 중에서 실제로 positive인 데이터의 비율을 정밀도라고 한다.
계산식은 아래와 같다.
Precision = TP / (TP + FP)정밀도는 모델이 positive로 예측한 데이터 중에서 실제로 positive인 데이터의 비율을 나타내므로,
신용카드 부정 사용, 스팸 메일 필터링과 같은 데이터 분류에서 유효성이 높다.
2-3. 재현율(Recall)
재현율은 실제로 positive인 데이터에 대해서 모델이 얼마나 positive 예측을 잘 했는 지 나타낸 지표이다.
계산식은 아래와 같다.
Recall = TP / (TP + FN)재현율은 데이터의 positive 값을 정확하게 분류하는 것이 중요할 경우에 사용된다.
실제 값이 positive인데 negative라고 잘못된 판단을 하면 안 되는 데이터 분류에서 유효성이 높다.
코로나 바이러스 감염 여부나 암 발생 유무를 예측해야 하는 데이터를 예로 들 수 있다.
2-4. F1-score
일반적으로, 정밀도와 재현율은 상호 보완적인 지표이기 때문에 한 쪽 수치를 높이면 다른 쪽 수치는 낮아진다.
이러한 이유로 정밀도와 재현율을 함께 고려할 수 있는 성능 지표가 필요하다.
F1-score는 정밀도와 재현율의 조화 평균으로 계산되기 때문에, 두 지표가 모두 높을 때 값이 높다.
F1-score = 2 * (Precision * Recall) / (Precision + Recall)
3. ROC곡선(Receiver Operating Characteristic Curve)
ROC곡선은 FPR(False Positive Rate)이 변할 때 TPR(True Positive Rate)이 변하는 정도를 나타낸 곡선이다.
여기서 TPR은 재현율을 나타내며, ROC곡선에서는 민감도(Sensitivity)라고 불린다.
TPR(=Recall) = TP / (TP + FN)이에 대비되는 지표로 특이성(Specificity)이라고 불리는 TNR(True Negative Rate)지표가 있다.
즉, TPR이 positive가 positive로 예측되는 것이 중요하다면, TNR은 negative가 negative로 예측되는 것이 중요한 지표이다.
TNR(특이성)은 다음과 같이 구할 수 있다.
TNR = TN / (TN + FP)이제 다시 ROC곡선으로 돌아가 보자.
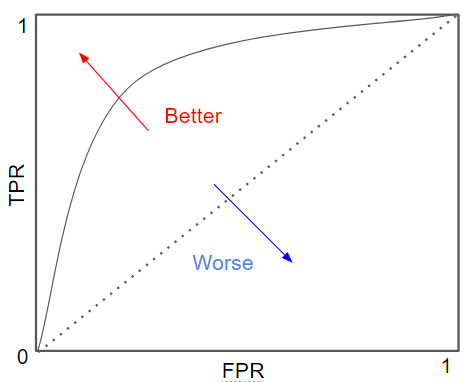
ROC곡선은 위와 같이 FPR(False Positive Rate)이 X축, TPR(민감도)가 Y축인 곡선이다.
TPR(민감도)는 위에서 구했고, FPR은 1-TNR(특이성)이다.
FPR = 1 - TNR
= FP / (FP + TN)
여러 용어가 나와서 헷갈리니 다시 한번 정리해 보자.
① TPR(True Positive Rate): positive인 데이터에 대해 positive로 정확하게 예측하는 비율(암 환자에게 암이라고 진단)
② FPR(False Positive Rate): negative인 케이스에 대해 positive로 틀리게 예측하는 비율(정상인에게 암이라고 진단)
여기서 FPR이 X축, TPR이 Y축이다.
일반적으로 ROC곡선 자체는 FPR과 TPR의 변화 값을 보는 데 이용하며, 분류의 성능 지표로 사용되는 것은 ROC 곡선 면적에 기반한 AUC(Area Under Curve) 값이다. 일반적으로 1에 가까울 수록 좋은 수치이므로, ROC곡선이 왼쪽 상단에 가까울수록 높은 성능을 나타낸다.

참고: 「파이썬 머신러닝 완벽 가이드」, 권철민 지음, 위키북스
'ML' 카테고리의 다른 글
| 선형회귀 평가지표 (with Scikit-learn) (0) | 2023.05.14 |
|---|---|
| Scikit-learn - 데이터 인코딩 (0) | 2023.04.08 |
| 피처 스케일링과 정규화 (0) | 2023.03.27 |
| 활성화 함수 구현하기 (0) | 2023.03.27 |
| 반응형 머신러닝 앱을 만드는 가장 빠른 방법 - gradio (0) | 2023.03.04 |




